Compute Wavelet Cross-Covariance Between Two Time Series

Computes wavelet cross-covariance or cross-correlation between two time series.

spin.covariance(x, y, lag.max = NA)
spin.correlation(x, y, lag.max = NA)

Arguments

x	first time series
y	second time series, same length as x
lag.max	maximum lag to compute cross-covariance (correlation)

Value

List structure holding the wavelet cross-covariances (correlations) according to scale.

Details

See references.

References

Gencay, R., F. Selcuk and B. Whitcher (2001) An Introduction to Wavelets and Other Filtering Methods in Finance and Economics, Academic Press.

Whitcher, B., P. Guttorp and D. B. Percival (2000) Wavelet analysis of covariance with application to atmospheric time series, Journal of Geophysical Research, 105, No. D11, 14,941-14,962.

See also

wave.covariance, wave.correlation.

Author

B. Whitcher

Examples

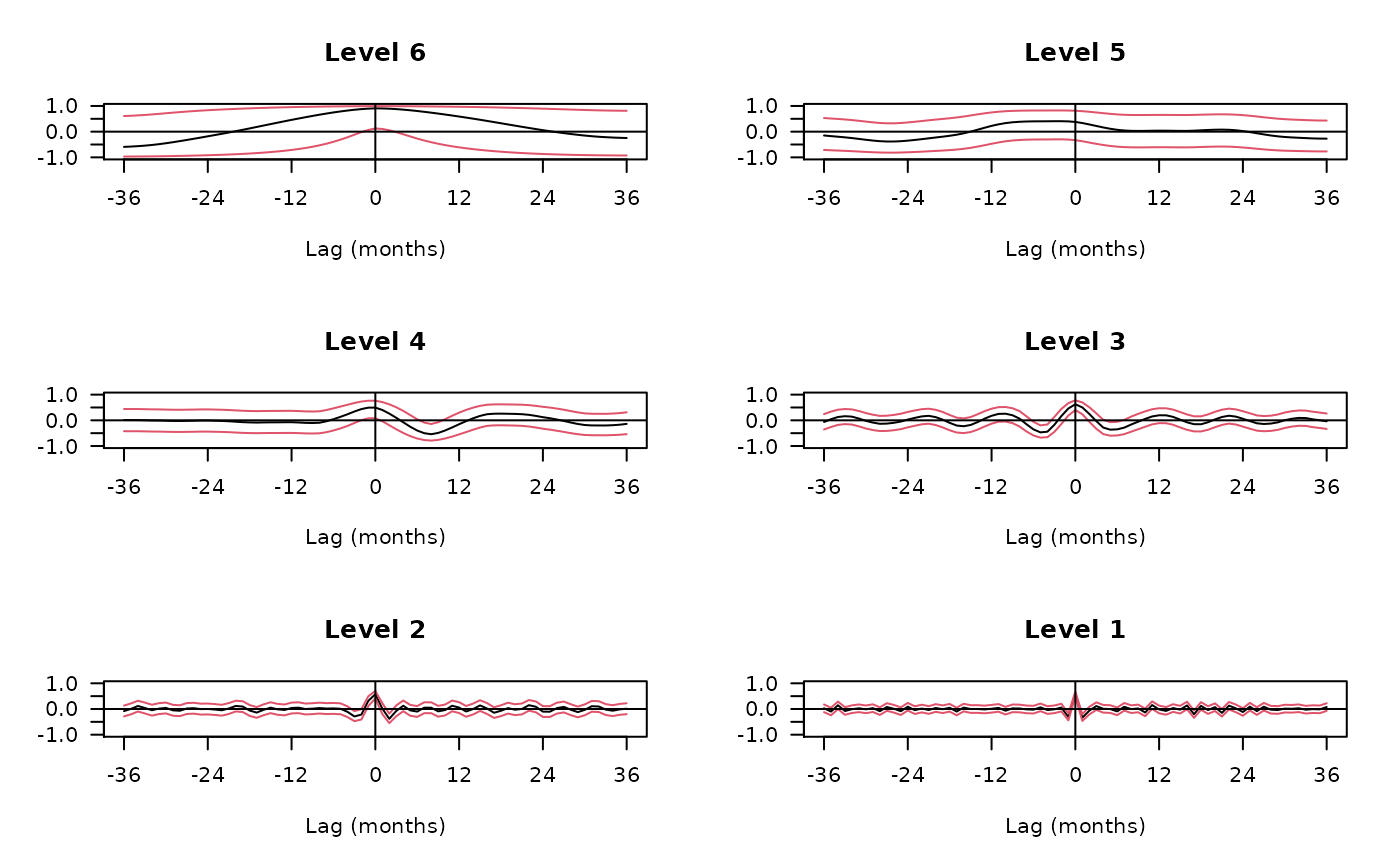
## Figure 7.9 from Gencay, Selcuk and Whitcher (2001)
data(exchange)
returns <- diff(log(exchange))
returns <- ts(returns, start=1970, freq=12)
wf <- "d4"
demusd.modwt <- modwt(returns[,"DEM.USD"], wf, 8)
demusd.modwt.bw <- brick.wall(demusd.modwt, wf)
jpyusd.modwt <- modwt(returns[,"JPY.USD"], wf, 8)
jpyusd.modwt.bw <- brick.wall(jpyusd.modwt, wf)
n <- dim(returns)[1]
J <- 6
lmax <- 36
returns.cross.cor <- NULL
for(i in 1:J) {
  blah <- spin.correlation(demusd.modwt.bw[[i]], jpyusd.modwt.bw[[i]], lmax)
  returns.cross.cor <- cbind(returns.cross.cor, blah)
}
returns.cross.cor <- ts(as.matrix(returns.cross.cor), start=-36, freq=1)
dimnames(returns.cross.cor) <- list(NULL, paste("Level", 1:J))
lags <- length(-lmax:lmax)
lower.ci <- tanh(atanh(returns.cross.cor) - qnorm(0.975) /
                 sqrt(matrix(trunc(n/2^(1:J)), nrow=lags, ncol=J, byrow=TRUE)
                      - 3))
upper.ci <- tanh(atanh(returns.cross.cor) + qnorm(0.975) /
                 sqrt(matrix(trunc(n/2^(1:J)), nrow=lags, ncol=J, byrow=TRUE)
                      - 3))
par(mfrow=c(3,2), las=1, pty="m", mar=c(5,4,4,2)+.1)
for(i in J:1) {
  plot(returns.cross.cor[,i], ylim=c(-1,1), xaxt="n", xlab="Lag (months)",
       ylab="", main=dimnames(returns.cross.cor)[[2]][i])
  axis(side=1, at=seq(-36, 36, by=12))
  lines(lower.ci[,i], lty=1, col=2)
  lines(upper.ci[,i], lty=1, col=2)
  abline(h=0,v=0)
}