Convolution of 3D Arrays using the Fourier Transform

Convolve a three-dimensinal array with another three-dimensional arry using the Fast Fourier Transform (FFT).

convFFT(A, B, C, FFTA = NULL)

Arguments

A	is a three-dimensional array (“the template”).
B	is a three-dimensional array (“the target”).
C	is a vector of length three (the center of “the template”).
FFTA	is the three-dimensional Fourier transform of `A`, this may save time when looping over multiple “targets”.

Value

A three-dimensional array, the same dimension as the input arrays, that is the convolution of the “target” to the “template” at all spatial locations.

Details

The arrays $A$ and $B$ are transformed into the Fourier domain and multiplied together (equivalent to a convolution in the image domain across all spatial locations simultaneously).

References

Briggs, W.L. and Henson, V.E. (1995) The DFT: An Owner's Manual for the Discrete Fourier Transform, SIAM: Philadelphia.

Author

Brandon Whitcher bwhitcher@gmail.com

Examples


cube <- array(0, c(20,20,1))
cube[9:12,9:12,1] <- 1
tkernel <- array(0, c(20,20,1))
tkernel[,,1] <- c(.5, 1, .5, rep(0,20-3)) %o% c(.5, 1, .5, rep(0,20-3))
tcenter <- findCenter(ifelse(tkernel > 0, TRUE, FALSE))
out <- convFFT(tkernel, cube, tcenter)
out[8:13,8:13,1]  ## text output
#>      [,1] [,2] [,3] [,4] [,5] [,6]
#> [1,] 0.25 0.75    1    1 0.75 0.25
#> [2,] 0.75 2.25    3    3 2.25 0.75
#> [3,] 1.00 3.00    4    4 3.00 1.00
#> [4,] 1.00 3.00    4    4 3.00 1.00
#> [5,] 0.75 2.25    3    3 2.25 0.75
#> [6,] 0.25 0.75    1    1 0.75 0.25

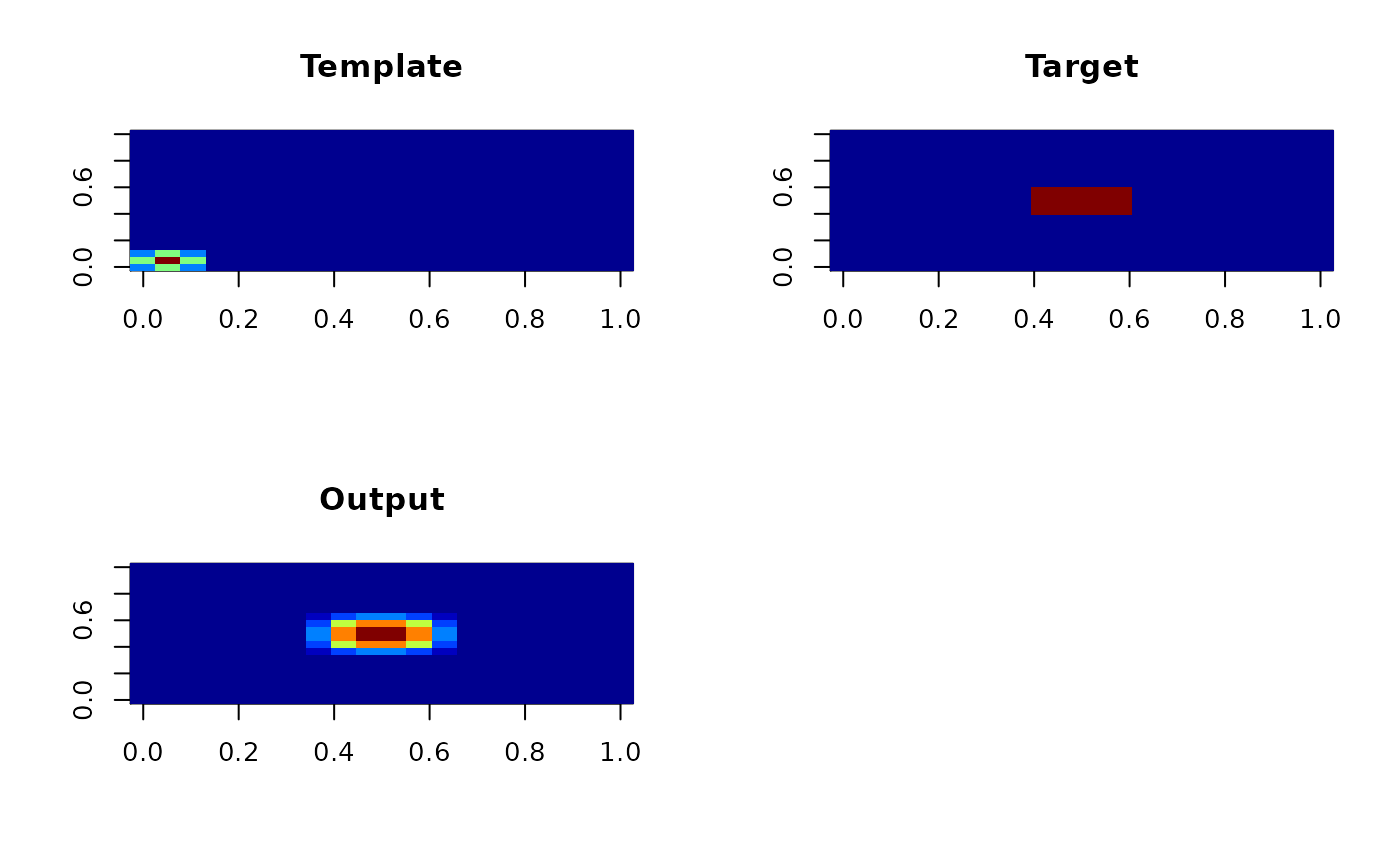
par(mfrow=c(2,2))  ## graphic output
image(drop(tkernel), col=oro.nifti::tim.colors(), main="Template")
image(drop(cube), col=oro.nifti::tim.colors(), main="Target")
image(drop(out), col=oro.nifti::tim.colors(), main="Output")