Estimate the Apparent Diffusion Coefficient (ADC)

Estimation of apparent diffusion coefficient (ADC) values, using a single exponential function, is achieved through nonlinear optimization.

ADC.fast(dwi, ...)

# S4 method for array
ADC.fast(
  dwi,
  bvalues,
  dwi.mask,
  control = minpack.lm::nls.lm.control(maxiter = 150),
  multicore = FALSE,
  verbose = FALSE
)

adc.lm(signal, b, guess, control = minpack.lm::nls.lm.control())

Arguments

dwi	Multidimensional array of diffusion-weighted images.
...	Additional variables defined by the method.
dwi.mask	Logical array that defines the voxels to be analyzed.
control	An optional list of control settings for `nls.lm`. See `nls.lm.control` for the names of the settable control values and their effect.
multicore	is a logical variable (default = `FALSE`) that allows parallel processing via parallel.
verbose	Additional information will be printed when `verbose=TRUE`.
signal	Signal intensity vector as a function of b-values.
b, bvalues	Diffusion weightings (b-values).
guess	Initial values of $S_0$ and $D$.

Value

A list structure is produced with estimates of $S_0$, $D$ and information about the convergence of the nonlinear optimization routine.

Details

The adc.lm function estimates parameters for a vector of observed MR signal intensities using the following relationship $$S(b) = S_0 \exp(-bD),$$ where $S_0$ is the baseline signal intensity and $D$ is the apparent diffusion coefficient (ADC). It requires the routine nls.lm that applies the Levenberg-Marquardt algorithm. Note, low b-values ($<50$ or $<100$ depending on who you read) should be avoided in the parameter estimation because they do not represent information about the diffusion of water in tissue.

The ADC.fast function rearranges the assumed multidimensional (2D or 3D) structure of the DWI data into a single matrix to take advantage of internal R functions instead of loops, and called adc.lm.

References

Buxton, R.B. (2002) Introduction to Functional Magnetic Resonance Imaging: Principles & Techniques, Cambridge University Press: Cambridge, UK.

Callahan, P.T. (2006) Principles of Nuclear Magnetic Resonance Microscopy, Clarendon Press: Oxford, UK.

Koh, D.-M. and Collins, D.J. (2007) Diffusion-Weighted MRI in the Body: Applications and Challenges in Oncology, American Journal of Roentgenology, 188, 1622-1635.

Author

Brandon Whitcher bwhitcher@gmail.com

Examples


S0 <- 10
b <- c(0, 50, 400, 800)  # units?
D <- 0.7e-3              # mm^2 / sec (normal white matter)

## Signal intensities based on the (simplified) Bloch-Torry equation
dwi <- function(S0, b, D) {
  S0 * exp(-b*D)
}

set.seed(1234)
signal <- array(dwi(S0, b, D) + rnorm(length(b), sd=0.15),
                c(rep(1,3), length(b)))
ADC <- ADC.fast(signal, b, array(TRUE, rep(1,3)))
unlist(ADC) # text output
#>           S0            D     S0.error      D.error 
#> 9.985900e+00 7.337532e-04 1.671637e+00 5.369434e+03 

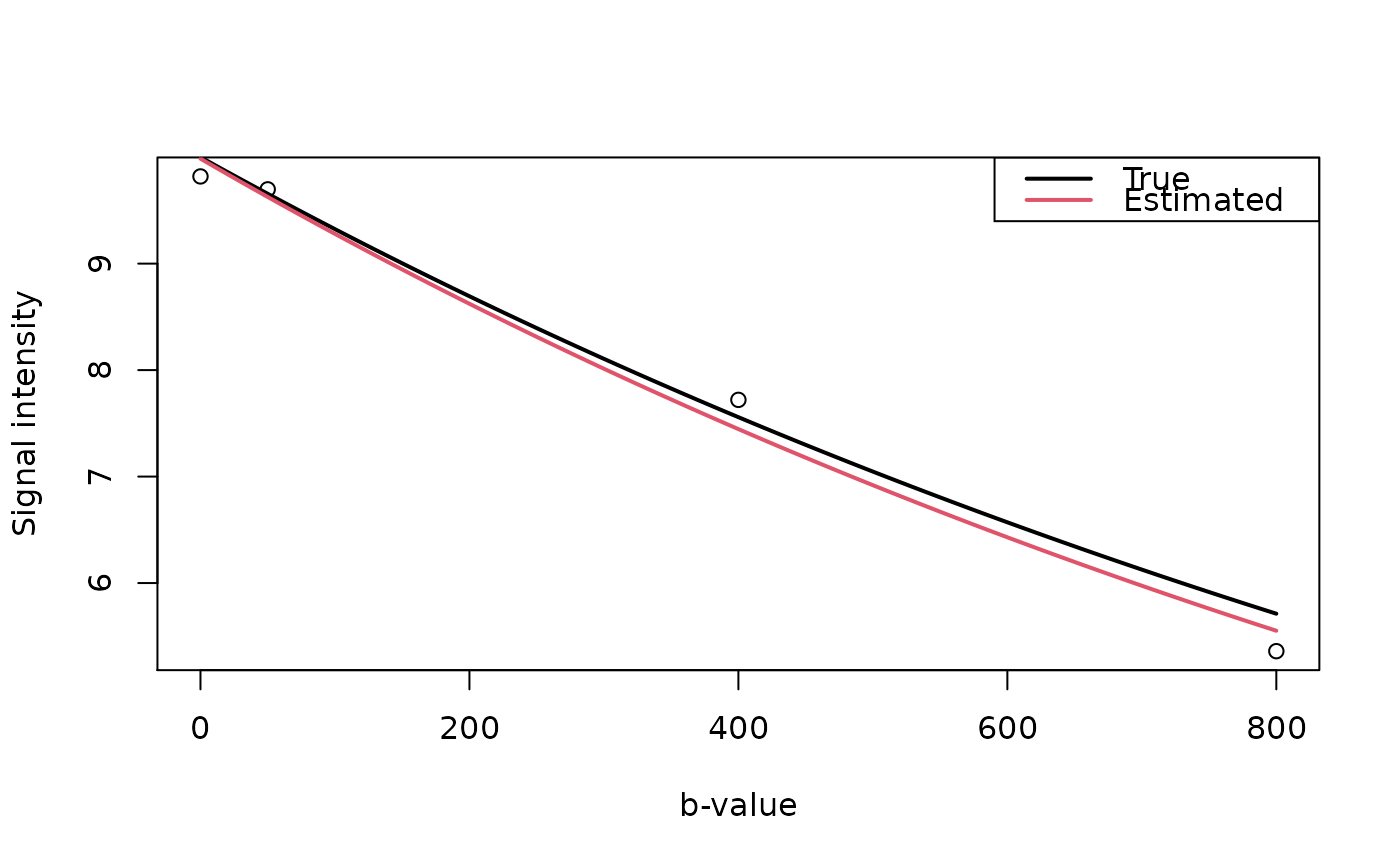
par(mfrow=c(1,1)) # graphical output
plot(b, signal, xlab="b-value", ylab="Signal intensity")
lines(seq(0,800,10), dwi(S0, seq(0,800,10), D), lwd=2, col=1)
lines(seq(0,800,10), dwi(c(ADC$S0), seq(0,800,10), c(ADC$D)), lwd=2, col=2)
legend("topright", c("True","Estimated"), lwd=2, col=1:2)