Functional mediation analysis under historical influence model

This function performs functional mediation regression under the historical influence model with given tuning parameter.

FMA.historical(Z, M, Y, delta.grid1 = 1, delta.grid2 = 1, delta.grid3 = 1, 
    intercept = TRUE, basis1 = NULL, Ld2.basis1 = NULL, basis2 = NULL, Ld2.basis2 = NULL, 
    basis.type = c("fourier"), nbasis1 = 3, nbasis2 = 3, 
    timeinv = c(0, 1), timegrids = NULL, 
    lambda1.m = 0.01, lambda2.m = 0.01, lambda1.y = 0.01, lambda2.y = 0.01)

Arguments

Z

a data matrix. Z is the treatment trajectory in the mediation analysis. The number of rows is the number of subjects, and the number of columns is the number of measured time points.
M

a data matrix. M is the mediator trajectory in the mediation analysis. The number of rows is the number of subjects, and the number of columns is the number of measured time points.
Y

a data matrix. Y is the outcome trajectory in the mediation analysis. The number of rows is the number of subjects, and the number of columns is the number of measured time points.
delta.grid1

a number indicates the width of treatment-mediator time interval in the mediator model.
delta.grid2

a number indicates the width of treatment-outcome time interval in the outcome model.
delta.grid3

a number indicates the width of mediator-outcome time interval in the outcome model.
intercept

a logic variable. Default is TRUE, an intercept term is included in the regression model.
basis1

a data matrix. Basis function on the \(s\) domain used in the functional data analysis. The number of columns is the number of basis function considered. If basis = NULL, Fourier basis functions will be generated.
Ld2.basis1

a data matrix. The second derivative of the basis function on the \(s\) domain. The number of columns is the number of basis function considered. If Ld2.basis = NULL, the second derivative of Fourier basis functions will be generated.
basis2

a data matrix. Basis function on the \(t\) domain used in the functional data analysis. The number of columns is the number of basis function considered. If basis = NULL, Fourier basis functions will be generated.
Ld2.basis2

a data matrix. The second derivative of the basis function on the \(t\) domain. The number of columns is the number of basis function considered. If Ld2.basis = NULL, the second derivative of Fourier basis functions will be generated.
basis.type

a character of basis function type. Default is Fourier basis (basis.type = "fourier").
nbasis1

an integer, the number of basis function on the \(s\) domain included. If basis1 is provided, this argument will be ignored.
nbasis2

an integer, the number of basis function on the \(t\) domain included. If basis2 is provided, this argument will be ignored.
timeinv

a numeric vector of length two, the time interval considered in the analysis. Default is (0,1).
timegrids

a numeric vector of time grids of measurement. If timegrids = NULL, it is assumed the between measurement time interval is constant.
lambda1.m

a numeric vector of tuning parameter values on the \(s\) domain in the mediator model.
lambda2.m

a numeric vector of tuning parameter values on the \(t\) domain in the mediator model.
lambda1.y

a numeric vector of tuning parameter values on the \(s\) domain in the outcome model.
lambda2.y

a numeric vector of tuning parameter values on the \(t\) domain in the outcome model.

Details

The historical influence mediation model is $$M(t)=\int_{\Omega_{t}^{1}}Z(s)\alpha(s,t)ds+\epsilon_{1}(t),$$ $$Y(t)=\int_{\Omega_{t}^{2}}Z(s)\gamma(s,t)ds+\int_{\Omega_{t}^{3}}M(s)\beta(s,t)ds+\epsilon_{2}(t),$$ where \(\alpha(s,t)\), \(\beta(s,t)\), \(\gamma(s,t)\) are coefficient curves; \(\Omega_{t}^{j}=[(t-\delta_{j})\vee 0,t]\) for \(j=1,2,3\). The model coefficient curves are estimated by minimizing the penalized \(L_{2}\)-loss.

Value

basis1

the basis functions on the \(s\) domain used in the analysis.

basis2

the basis functions on the \(t\) domain used in the analysis.

M

a list of output for the mediator model coefficient: the estimated coefficient with respect to the basis function curve: the estimated coefficient curve fitted: the fitted value of M lambda1: the \(\lambda\) value on the \(s\) domain lambda2: the \(\lambda\) value on the \(t\) domain

Y

a list of output for the outcome model coefficient: the estimated coefficient with respect to the basis function curve: the estimated coefficient curve fitted: the fitted value of Y lambda1: the \(\lambda\) value on the \(s\) domain lambda2: the \(\lambda\) value on the \(t\) domain

IE

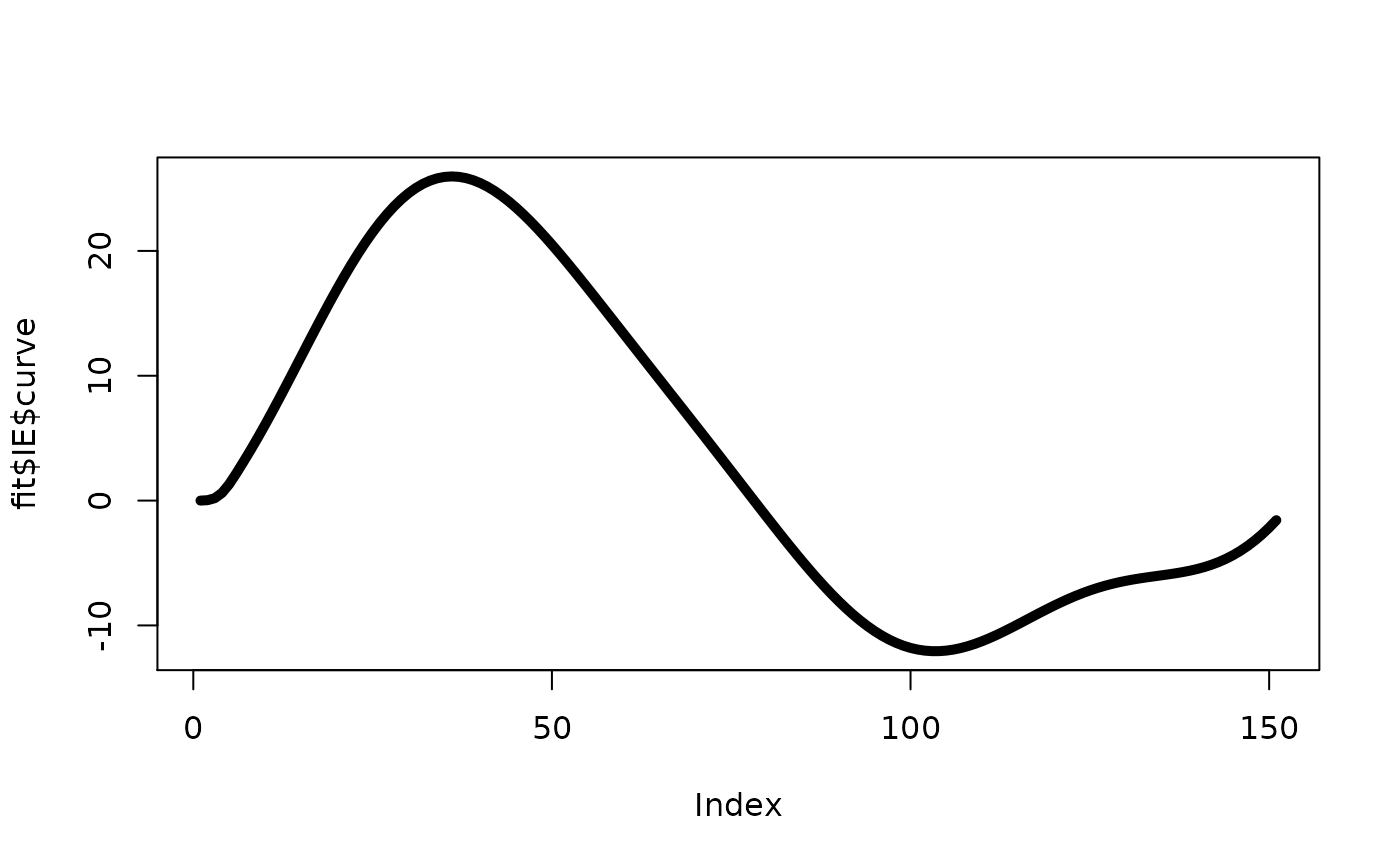
a list of output for the indirect effect comparing \(Z_{1}(t)=1\) versus \(Z_{0}(t)=0\) curve: the estimated causal curve

DE

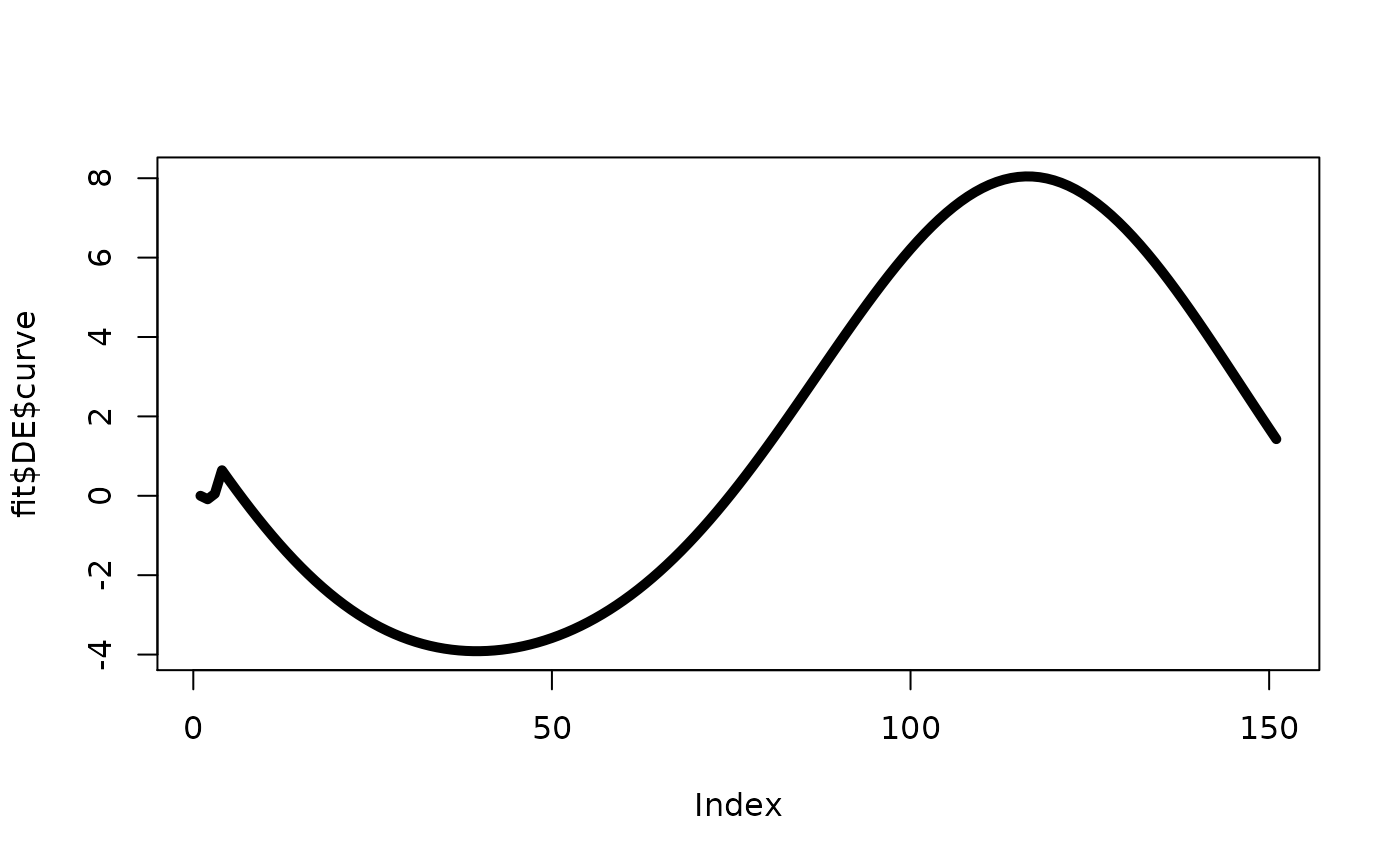
a list of output for the direct effect comparing \(Z_{1}(t)=1\) versus \(Z_{0}(t)=0\) curve: the estimated causal curve

References

Zhao et al. (2017). Functional Mediation Analysis with an Application to Functional Magnetic Resonance Imaging Data. arXiv preprint arXiv:1805.06923.

Author

Yi Zhao, Johns Hopkins University, zhaoyi1026@gmail.com;

Xi Luo, Brown University xi.rossi.luo@gmail.com;

Martin Lindquist, Johns Hopkins University, mal2053@gmail.com;

Brian Caffo, Johns Hopkins University, bcaffo@gmail.com

Examples


##################################################
# Historical influence functional mediation model
data(env.historical)
Z<-get("Z",env.historical)
M<-get("M",env.historical)
Y<-get("Y",env.historical)

# consider Fourier basis
fit<-FMA.historical(Z,M,Y,delta.grid1=3,delta.grid2=3,delta.grid3=3,
    intercept=FALSE,timeinv=c(0,300))

# estimate of causal curves
plot(fit$IE$curve,type="l",lwd=5)

plot(fit$DE$curve,type="l",lwd=5)

##################################################