Functional mediation analysis under concurrent regression model
FMA.concurrent.RdThis function performs functional mediation regression under the concurrent model with given tuning parameter.
FMA.concurrent(Z, M, Y, intercept = TRUE, basis = NULL, Ld2.basis = NULL,
basis.type = c("fourier"), nbasis = 3, timeinv = c(0, 1), timegrids = NULL,
lambda.m = 0.01, lambda.y = 0.01)Arguments
| Z | a data matrix. |
|---|---|
| M | a data matrix. |
| Y | a data matrix. |
| intercept | a logic variable. Default is |
| basis | a data matrix. Basis function used in the functional data analysis. The number of columns is the number of basis function considered. If |
| Ld2.basis | a data matrix. The second derivative of the basis function. The number of columns is the number of basis function considered. If |
| basis.type | a character of basis function type. Default is Fourier basis ( |
| nbasis | an integer, the number of basis function included. If |
| timeinv | a numeric vector of length two, the time interval considered in the analysis. Default is (0,1). |
| timegrids | a numeric vector of time grids of measurement. If |
| lambda.m | a numeric value of the tuning parameter in the mediator model. |
| lambda.y | a numeric value of the tuning parameter in the outcome model. |
Details
The concurrent mediation model is $$M(t)=Z(t)\alpha(t)+\epsilon_{1}(t),$$ $$Y(t)=Z(t)\gamma(t)+M(t)\beta(t)+\epsilon_{2}(t),$$ where \(\alpha(t)\), \(\beta(t)\), \(\gamma(t)\) are coefficient curves. The model coefficient curves are estimated by minimizing the penalized \(L_{2}\)-loss.
Value
the basis functions used in the analysis.
a list of output for the mediator model coefficientthe estimated coefficient with respect to the basis function curve: the estimated coefficient curve fitted: the fitted value of M lambda: \(\lambda\) value
a list of output for the outcome model coefficient: the estimated coefficient with respect to the basis function curve: the estimated coefficient curve fitted: the fitted value of Y lambda: \(\lambda\) value
a list of output for the indirect effect comparing \(Z_{1}(t)=1\) versus \(Z_{0}(t)=0\) coefficients: the coefficient with respect to the basis function curve: the estimated causal curve
a list of output for the direct effect comparing \(Z_{1}(t)=1\) versus \(Z_{0}(t)=0\) coefficients: the coefficient with respect to the basis function curve: the estimated causal curve
References
Zhao et al. (2017). Functional Mediation Analysis with an Application to Functional Magnetic Resonance Imaging Data. arXiv preprint arXiv:1805.06923.
Author
Yi Zhao, Johns Hopkins University, zhaoyi1026@gmail.com;
Xi Luo, Brown University xi.rossi.luo@gmail.com;
Martin Lindquist, Johns Hopkins University, mal2053@gmail.com;
Brian Caffo, Johns Hopkins University, bcaffo@gmail.com
Examples
##################################################
# Concurrent functional mediation model
data(env.concurrent)
Z<-get("Z",env.concurrent)
M<-get("M",env.concurrent)
Y<-get("Y",env.concurrent)
# consider Fourier basis
fit<-FMA.concurrent(Z,M,Y,intercept=FALSE,timeinv=c(0,300))
# estimate of alpha
plot(fit$M$curve[1,],type="l",lwd=5)
lines(get("alpha",env.concurrent),lty=2,lwd=2,col=2)
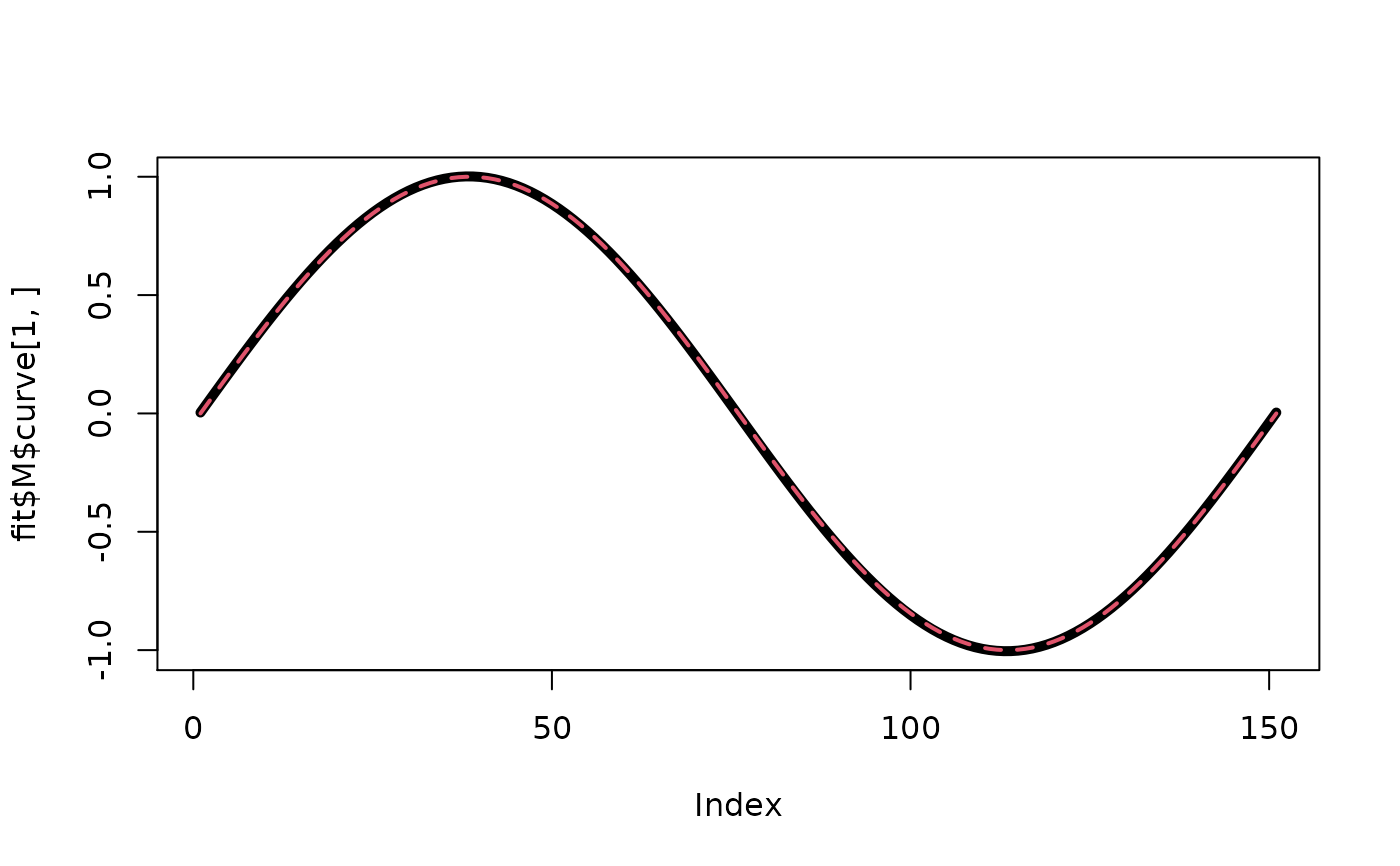 # estimate of gamma
plot(fit$Y$curve[1,],type="l",lwd=5)
lines(get("gamma",env.concurrent),lty=2,lwd=2,col=2)
# estimate of gamma
plot(fit$Y$curve[1,],type="l",lwd=5)
lines(get("gamma",env.concurrent),lty=2,lwd=2,col=2)
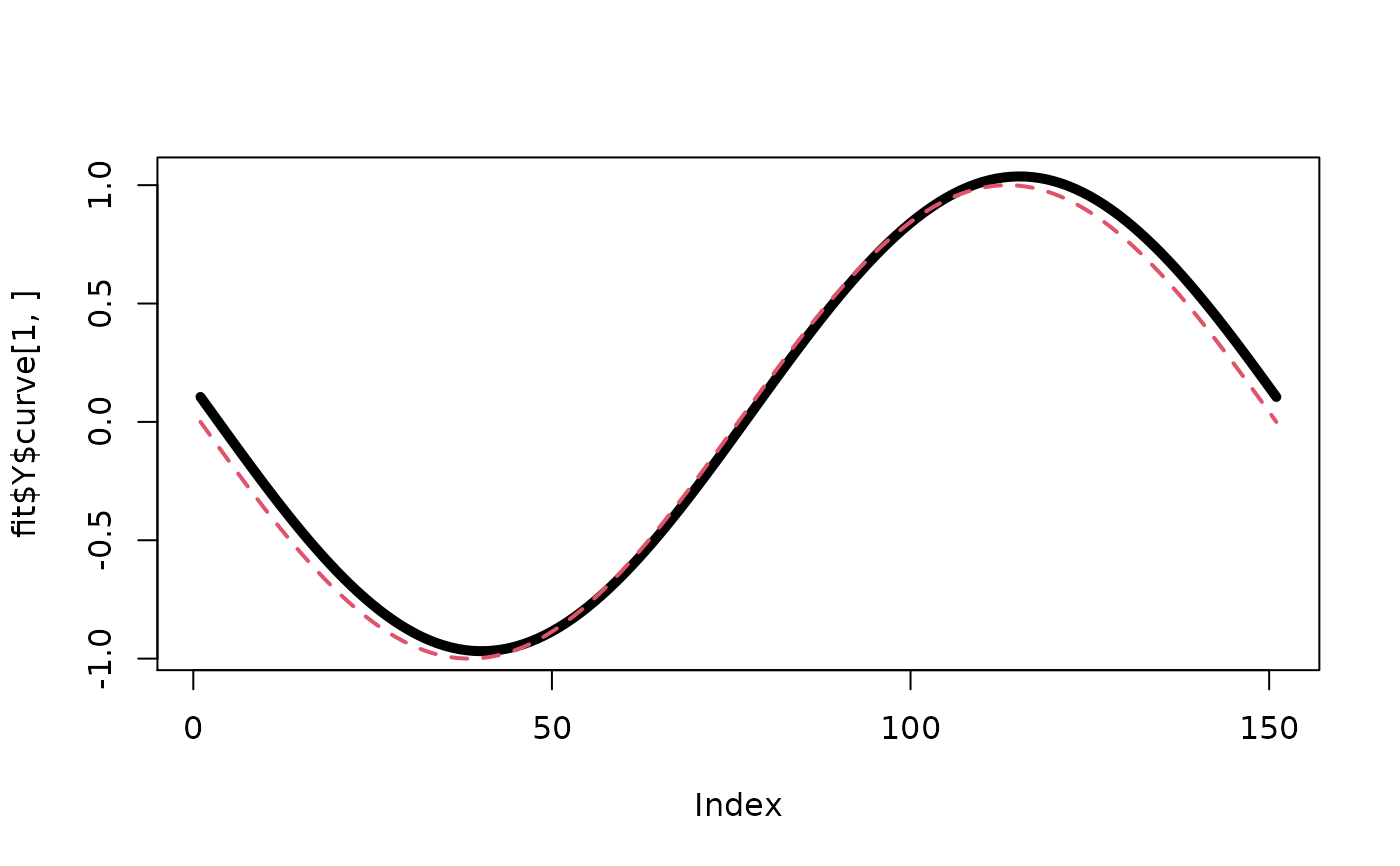 # estimate of beta
plot(fit$Y$curve[2,],type="l",lwd=5)
lines(get("beta",env.concurrent),lty=2,lwd=2,col=2)
# estimate of beta
plot(fit$Y$curve[2,],type="l",lwd=5)
lines(get("beta",env.concurrent),lty=2,lwd=2,col=2)
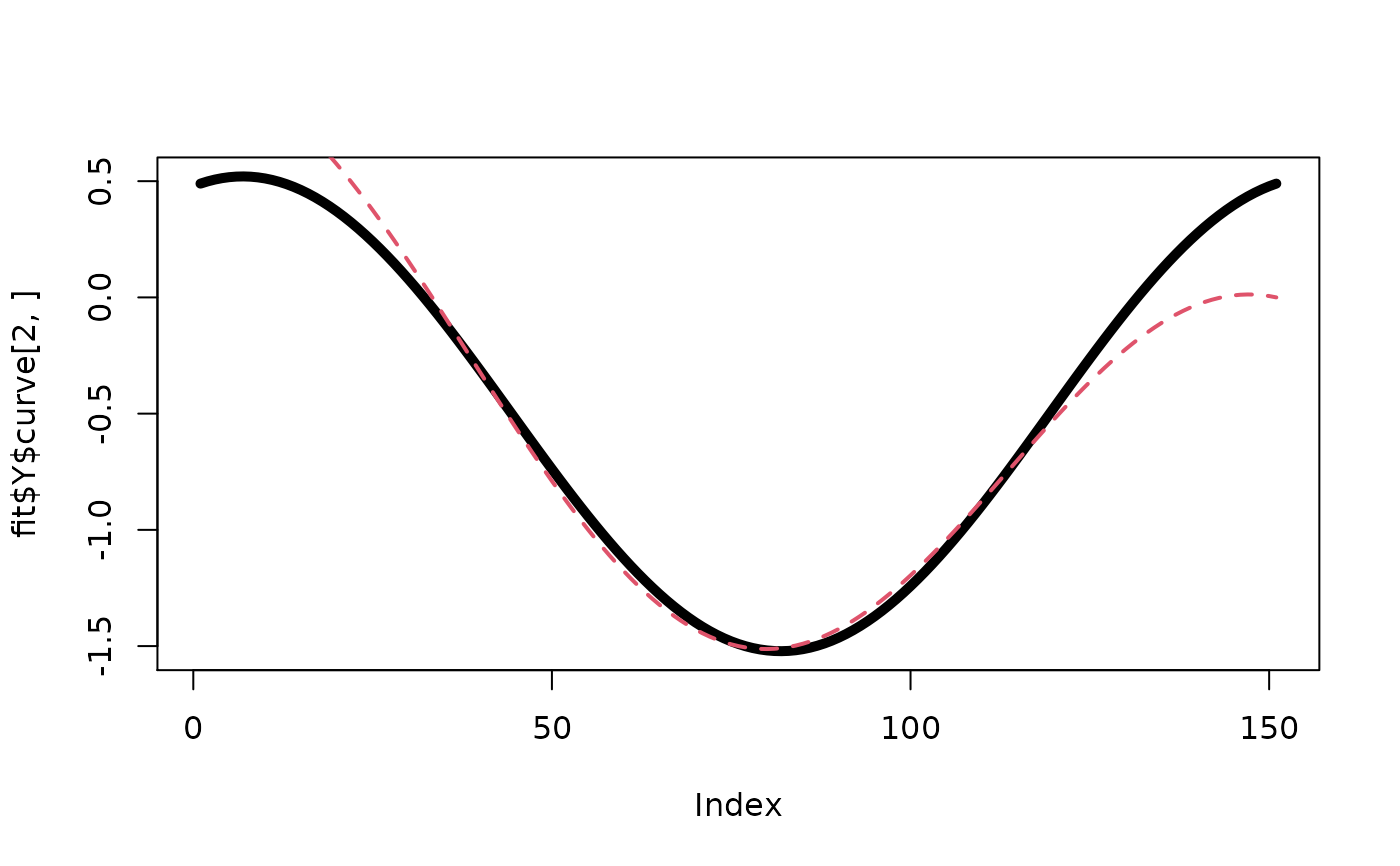 # estimate of causal curves
plot(fit$IE$curve,type="l",lwd=5)
# estimate of causal curves
plot(fit$IE$curve,type="l",lwd=5)
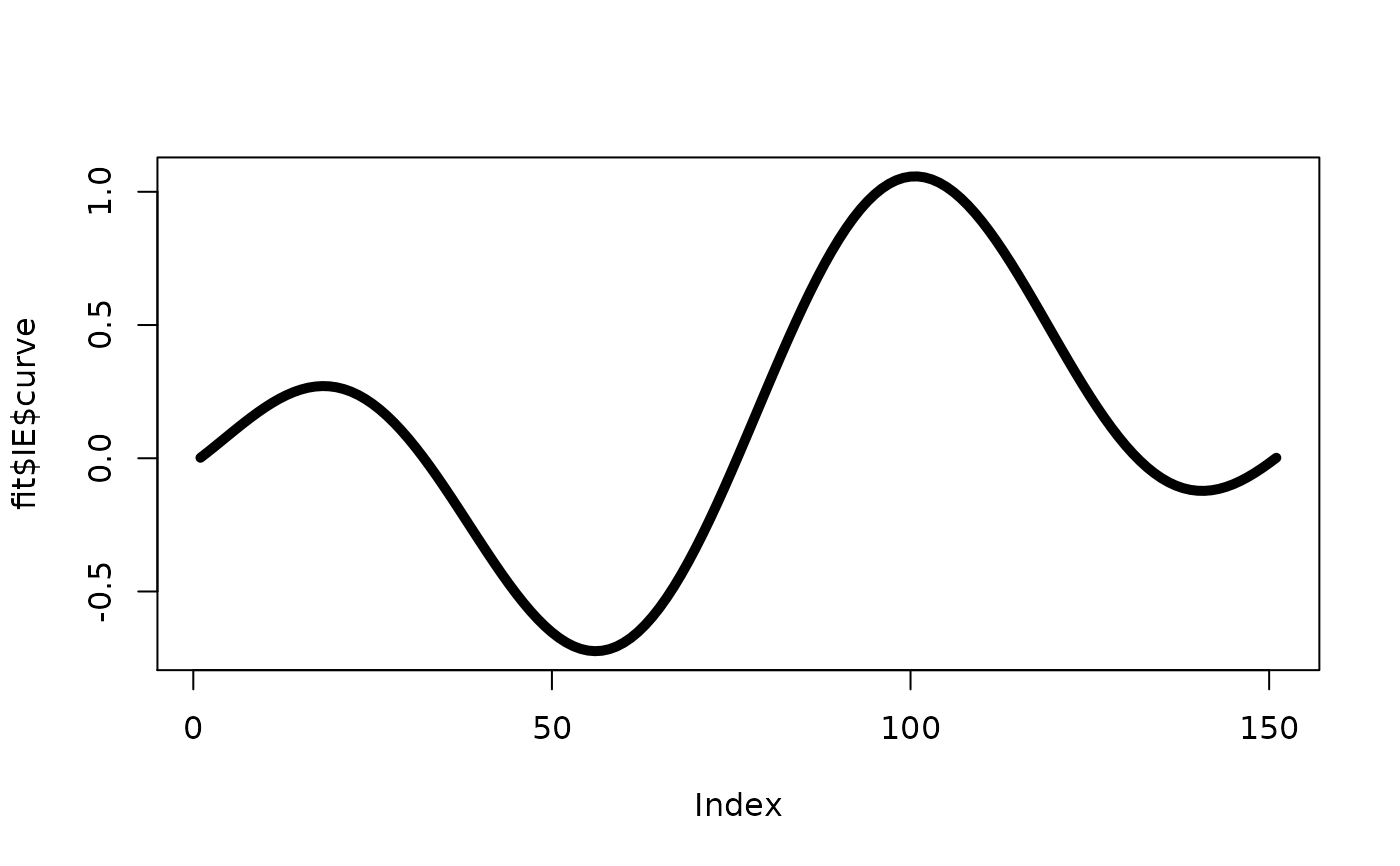 plot(fit$DE$curve,type="l",lwd=5)
plot(fit$DE$curve,type="l",lwd=5)
 ##################################################
##################################################